チューブが狭くなる中央のセクションを除いて、一定の直径を持つ滑らかな丸いチューブに空気が送り込まれているとします。直径の半分まで下げてから、再び広げます。直径のすべての変化がスムーズに行われ、空気が乱気流や乱流なしでチューブを安定して流れると仮定します。
運動
チューブのどこに期待しますか圧力が最大になるのですか?
回答
ほとんどの人が初めてこれを尋ねたところ、圧力はチューブの狭い部分で最大になると予測されていました。しかし、実際に実験を行うと、チューブに沿ったさまざまなポイントに圧力計を配置することで、直感に反して、空気が最も速く移動している場所で空気圧が最も低いことがわかります!

これがどのようになるかを確認するために、静止流体内の圧力がどのように変化するかを見つけるために開発した手法。私たちがそれを行った方法は、覚えておいてください、流体の小さな円柱の自由体図を描くことでした。この小さなシリンダーは静止していたので、それにかかる総力はゼロであり、正味の圧力が重量のバランスを取りました。次に、着実に移動する流体について考えます。流線、線を描画して流れを視覚化すると便利です。線の方向は、各ポイントで流体が移動する方向になります。

実際、これらの流線は、流体が移動する方向を示すだけでなく、速度の概念も示します。同じ量の流体が流れているため、これらが互いに近づくと、流体はより速く移動する必要があります。より狭い領域を通して。ここで、パイプに沿って移動する空気の円柱を想像してみてください。その軸は流線に平行です。明らかに、チューブの狭い部分に入るときに速度を上げる必要があります。狭い部分には広い部分と同じ量の空気が流れるため、速くなる必要があります。
ただし、小さい場合は流体のシリンダーが加速しているので、後ろから押す力で作用する必要があります。
水平方向に移動するため、ここでは重量は関係ありません。したがって、それに作用する力は圧力だけであり、背面の圧力は前面の圧力よりも大きいと結論付ける必要があります。したがって、狭い部分に入ると圧力が低下している必要があります。何が起こっているのかを明確にするために、かなり大きな円柱を描きます。
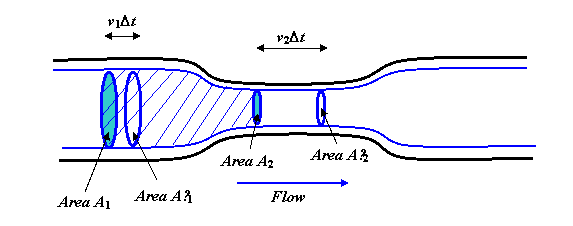
流体は着実かつスムーズに流れています。パイプ。太い青い線は流線です。実際、図全体を中心軸を中心に回転させて3次元画像を取得することを想像してください。青い線は円柱になり、「ネック」セクションが狭くなり、の形状が反映されます。パイプ。
ここで、示されている流線内の流体の本体を検討し、両端が円形の領域A1とA2で覆われていることを確認します。A1を横切る流体の流量は、定常流では流体が中央に堆積する(またはそこから枯渇する)ことができないため、A2を横切る流れ。1秒間にA1を横切る体積はv1A1です(これを確認するには、細いパイプのない長い直線パイプを想像してください)。部分。流体がたとえば毎秒3メートルで流れている場合、1秒で、上流側の領域A1から3メートル以内にあったすべての流体が流れます。)
つまり、 A1を横切る流れはA2を横切る流れに等しい\
(脚注:暗黙的に速度を仮定していることは言及する価値がありますtyは、エリアA1のすべてのポイントで同じです。実際の流体にはある程度の粘性(摩擦)があり、パイプの中央よりも側面の近くでゆっくりと移動します。これについては後で説明します。今のところ、粘度を無視するときに使用される「理想的な」流体を検討します。実際、得られた結果は問題ありません。側面から離れた小さな領域A1をとることができたので、速度は次のようになります。領域全体で同じですが、それでは図がはるかに明確になりません。)
これで、流体が狭い部分に加速するときの流体の運動エネルギーの増加を調べる準備ができました。圧力差が速度を上げるために必要な仕事をどのように行ったかを理解します。
\
このエネルギー増加の唯一の原因は、流体を押し込む際の圧力によって行われる仕事です。狭い部分。
\
つまり、これは流体が後ろから押すことによって流体のチャンクに対して行われる作業ですが、これで話は終わりではありません。流体自体はその前にある流体を押す働きをするので、チャンクのエネルギーの全体的な増加を見つけるには、それが行う外部の仕事を差し引く必要があります。つまり、流体への圧力によって行われる作業の合計は
\
\(A_1v_1 = A_2v_2 \)であることを思い出してください。
行われるこの作業は等しくなければなりません 運動エネルギーの変化なので、
\
そこから
\
これはベルヌーイの方程式です。
\。
寄稿者と寄稿者
- Michael Fowler(バージニア大学物理学部ビーム教授)