理想気体での断熱膨張と圧縮中の体積変化に伴って圧力はどのように変化しますか?このページは、サウンドに関するディスカッションの付録です。大気圧の空気はほぼ理想気体であり、空気中の音の伝達は、通常の周波数と伝達距離では断熱に近いです。 (以下でこの仮定に戻ります。)
熱力学の第1法則は、内部エネルギーdUの変化を、システムによって実行される仕事dWとそれに追加される熱dQに関連付けます。
dU = dQ – dW
定義上、断熱プロセスでは、熱交換dQ = 0.これを最初の法則に置き換えて再配置すると、
0 = dQ = dU + dW
第2項は簡単です。システムがボリュームVをdVだけ変更したときにdWで行われる仕事は、PdVです。
最初の項は比熱に関連している場合があります。比熱は、物質1モルあたりの単位温度変化ごとに追加される熱として定義されます。一定の体積で熱を加えると、ガスは膨張しないため、機能しません。したがって、加えられた熱は内部エネルギーUを増加させます。したがって、一定の体積での比熱は、ここでnはモル数です。したがって
これで、理想的なガスの状態方程式は
nRT = PV( ii)
ここで、Rはガス定数です。導関数をとると
ここで、式(i)と(iii)を組み合わせてTを削除します。(i)および(ii)ncvdTに対してそれぞれ次の式を指定します。
PdVとVdPの用語を収集すると、
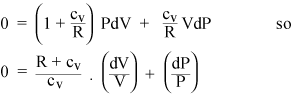
これで、気体が理想的な場合、その内部エネルギーはすべて運動エネルギーであるため、内部エネルギーUはTのみに依存します。理想気体の状態方程式(ii)から、次のように計算できます。一定の圧力で行われる作業dW:それはPdV = nRdTです。したがって、一定の圧力でガスに熱を加える場合、一定の体積で加える必要のある熱を超えて、ガスのモルごとにRdTを追加で加熱する必要があります。したがって、一定圧力での理想気体の比熱は、cP = cv + Rです。比熱の比には、標準記号
が与えられます。つまり、
(iv)
これは、音波について説明する必要がある主な結果です。圧力の比例変化が、体積の比例変化のγ倍または密度の比例変化のγ倍であることを示しました。
ただし、重要な結果から数行しか離れていないため、ここで停止しません。d(ln x)= dx / xであることがわかっています(証明については計算を参照してください)。上記の式は
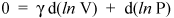
そしてそれを再配置して与える
(v)
したがって、理想的なガスでの断熱プロセスのために
。(vi)
振り返ってみると、cP > cV:At一定のボリューム、すべてのthあなたが入れた熱は、内部エネルギーを増加させ、それによって温度を上昇させることになります。一定の圧力では、内部エネルギーを上昇させる熱だけでなく、システムが熱膨張するときに行われる仕事に等しい量の熱も投入する必要があります。空気の場合、γは約1.4です。
もちろん、状態方程式(ii)から(vi)に代入して、PとTまたはTとVが断熱過程にどのように関連しているかを確認することもできます。
音が断熱されるのはいつですか?
「空気中の音の伝達は、通常の周波数と伝達距離では断熱に近い」と前述しました。これはいつ失敗しますか?音波の最大圧力では、温度が高くなります。したがって、ある程度の熱が隣接する最小圧力に拡散すると予想されます。もちろん、音波の半周期では、熱が半波長を拡散する時間はあまりありません。ただし、熱が拡散するのにかかる時間は、距離の2乗になります。したがって、短い半波長は短い半周期を補う以上のものであるため、このプロセスは高周波では無視できません。この拡散は、特に高周波で波から機械的エネルギーを取り除き、その効果は伝送距離とともに増加します。このため(場合によっては他の理由もありますが)、遠くの音は近くの音よりも音量が小さいだけでなく、明るさも小さくなります。