を使用した幅優先探索(BFS)アルゴリズムBFSアルゴリズム(幅優先探索)とは何ですか?
幅優先探索(BFS)は、データのグラフ化、ツリーの検索、または構造のトラバースに使用されるアルゴリズムです。 BFSの完全な形式は、幅優先探索です。
アルゴリズムは、グラフ内のすべての主要ノードに効率的にアクセスして、正確な幅広の方法でマークを付けます。このアルゴリズムは、グラフ内の単一のノード(初期ポイントまたはソースポイント)を選択してから、選択したノードに隣接するすべてのノードにアクセスします。 BFSはこれらのノードに1つずつアクセスすることを忘れないでください。
アルゴリズムが開始ノードにアクセスしてマークを付けると、最も近い未アクセスのノードに向かって移動し、それらを分析します。訪問すると、すべてのノードがマークされます。これらの反復は、グラフのすべてのノードに正常にアクセスしてマークが付けられるまで続きます。
このアルゴリズムのチュートリアルでは、次のことを学習します。
- BFSアルゴリズム(幅優先探索)とは何ですか?
- グラフ走査とは何ですか?
- BFSアルゴリズムのアーキテクチャ
- なぜBFSアルゴリズムが必要なのですか?
- BFSアルゴリズムはどのように機能しますか?
- BFSアルゴリズムの例
- BFSアルゴリズムのルール
- BFSアルゴリズムのアプリケーション
グラフトラバーサルとは何ですか?
グラフトラバーサルは、グラフ内の頂点位置を特定するために一般的に使用される方法です。これは、訪問した頂点のシーケンスをマークするとともに、グラフを速度と精度で分析できる高度な検索アルゴリズムです。このプロセスにより、無限ループに閉じ込められることなく、グラフ内の各ノードにすばやくアクセスできます。
BFSアルゴリズムのアーキテクチャ
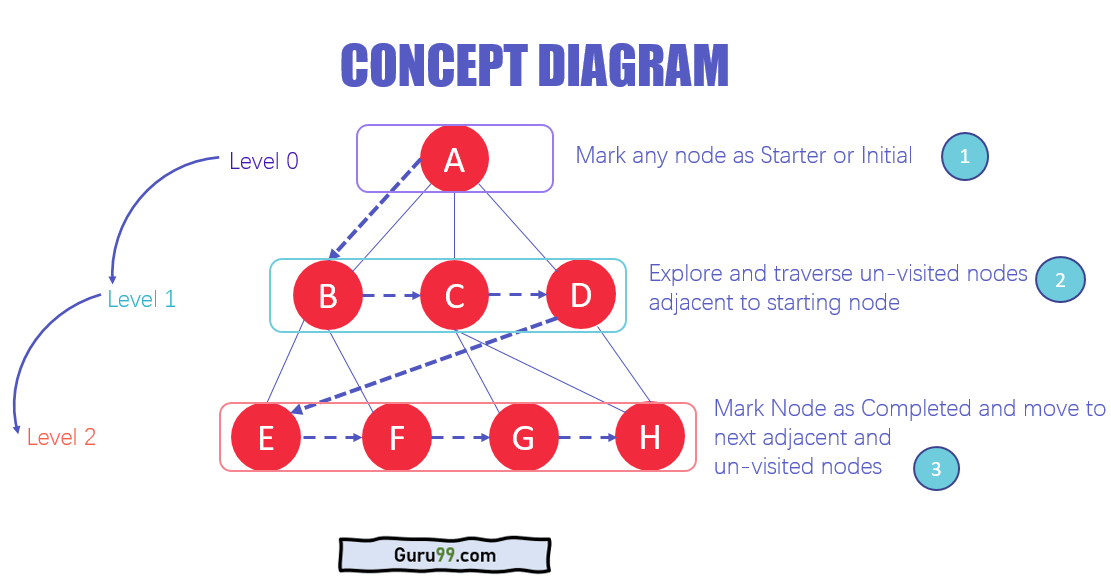
- データのさまざまなレベルで、任意のノードを開始としてマークできますまたはトラバースを開始する最初のノード。 BFSはノードにアクセスし、訪問済みとしてマークしてキューに配置します。
- これで、BFSは最も近い未訪問のノードにアクセスし、それらにマークを付けます。これらの値もキューに追加されます。キューはFIFOモデルで機能します。
- 同様の方法で、グラフ上の残りの最も近いノードと訪問されていないノードがマークされて分析され、キューに追加されます。これらのアイテムは、受信時にキューから削除され、結果として出力されます。
なぜBFSアルゴリズムが必要なのですか?
データセットの検索にBFSアルゴリズムを使用する理由はたくさんあります。このアルゴリズムを最初に選択する最も重要な側面のいくつかは次のとおりです。
- BFSは、グラフ内のノードを分析し、これらを通過する最短パスを構築するのに役立ちます。
- BFSは、最小の反復回数でグラフをトラバースできます。
- BFSアルゴリズムのアーキテクチャはシンプルで堅牢です。
- BFSアルゴリズムの結果は、他のアルゴリズムと比較して高レベルの精度を保持しています。
- BFSの反復はシームレスであり、このアルゴリズムが無限ループの問題に巻き込まれる可能性はありません。
BFSアルゴリズムはどのように機能しますか?
グラフトラバーサルでは、ツリーのような構造で、アクセスされていないすべてのノードにアクセス、チェック、更新するアルゴリズムが必要です。グラフ走査は、グラフ上のノードにアクセスする順序によって分類されます。
BFSアルゴリズムは、グラフの最初のノードまたは開始ノードから操作を開始し、それを完全にトラバースします。最初のノードを正常にトラバースすると、グラフ内のトラバースされていない次の頂点にアクセスしてマークが付けられます。
したがって、現在の頂点に隣接するすべてのノードが最初の反復で訪問され、トラバースされたと言えます。単純なキュー手法を使用してBFSアルゴリズムの動作を実装し、次のステップで構成されます。
ステップ1)

グラフ内の各頂点またはノードは既知です。たとえば、ノードをVとしてマークできます。
ステップ2)

頂点Vにアクセスしない場合は、頂点VをBFSキューに追加します
ステップ3)

BFS検索を開始し、完了後、頂点Vを訪問済みとしてマークします。
ステップ4)

BFSキューはまだ残っています空ではないため、グラフの頂点Vをキューから削除します。
ステップ5)

残りのすべての頂点を取得します頂点Vに隣接するグラフ上
ステップ6)

隣接する頂点ごとに、たとえばV1がまだアクセスされていない場合は、V1をBFSキューに追加します。
ステップ7)

BFSはV1にアクセスし、アクセス済みとしてマークしてキューから削除します。
BFSアルゴリズムの例
ステップ1)

次のグラフがあります0〜6の範囲の7つの数値。
ステップ2)

0またはゼロがルートノードとしてマークされています。
ステップ3)

0にアクセスし、マークを付けて、キューデータ構造に挿入します。
ステップ4)
残りの0個の隣接ノードと未訪問ノードが訪問され、マークが付けられ、キューに挿入されます。
ステップ5)

すべてのノードにアクセスするまで、トラバースの反復が繰り返されます。
BFSアルゴリズムのルール
BFSアルゴリズムを使用するための重要なルールは次のとおりです。
- キュー(FIFO-先入れ先出し)データ構造BFSによって使用されます。
- グラフ内の任意のノードをルートとしてマークし、そこからデータのトラバースを開始します。
- BFSはグラフ内のすべてのノードをトラバースし、完了したものとしてそれらをドロップし続けます。
- BFSは隣接する未訪問のノードにアクセスし、完了としてマークして、キューに挿入します。
- 隣接する頂点が見つからない場合、前の頂点をキューから削除します。
- BFSアルゴリズムは、グラフ内のすべての頂点が正常にトラバースされ、完了としてマークされるまで繰り返されます。
- どのノードからのデータのトラバース中にもBFSによって引き起こされるループはありません。
BFSアルゴリズムのアプリケーション
BFSアルゴリズムの実装が非常に効果的である可能性がある実際のアプリケーションのいくつかを見てください。
- 重み付けされていないグラフ:BFSアルゴリズムは、すべてを訪問するための最短パスと最小スパンツリーを簡単に作成できます。グラフの頂点を可能な限り短い時間で高精度に。
- P2Pネットワーク:BFSを実装して、ピアツーピアネットワーク内の最も近いノードまたは隣接するノードをすべて見つけることができます。これにより、必要なデータをより迅速に見つけることができます。 。
- Webクローラー:検索エンジンまたはWebクローラーは、BFSを使用することで、複数レベルのインデックスを簡単に構築できます。BFSの実装は、Webページであるソースから開始し、そのソースからのすべてのリンクにアクセスします。 。
- ナビゲーションシステム:BFSは、メインまたはソースの場所からすべての隣接する場所を見つけるのに役立ちます。
- ネットワークブロードキャストing:ブロードキャストされたパケットは、BFSアルゴリズムによってガイドされ、アドレスを持つすべてのノードを見つけて到達します。
概要
- グラフトラバーサルは、アルゴリズムが訪問、チェック、および/または訪問されていないすべてのノードを更新する必要がある独自のプロセスです。木のような構造。 BFSアルゴリズムも同様の原理で機能します。
- このアルゴリズムは、グラフ内のノードを分析し、これらを通過する最短パスを構築するのに役立ちます。
- アルゴリズムは、最小の反復回数と最短の時間でグラフをトラバースします。
- BFSは、グラフ内の単一のノード(初期ポイントまたはソースポイント)を選択してから、選択したノードに隣接するすべてのノードにアクセスします。 BFSはこれらのノードに1つずつアクセスします。
- 訪問されマークされたデータは、BFSによってキューに入れられます。キューは先入れ先出し方式で機能します。したがって、最初にグラフに配置された要素が最初に削除され、結果として出力されます。
- BFSアルゴリズムが無限ループに陥ることはありません。
- 高精度で堅牢な実装により、BFSはP2Pネットワーク、Webクローラーなどの複数の実際のソリューションで使用されます。およびネットワークブロードキャスト。