テブナンの定理は、どんなに複雑な線形回路でも、単一の電圧源と負荷に接続された直列抵抗を備えた等価回路に単純化できると述べています。 「線形」の資格は、重ね合わせの原理に見られるものと同じです。ここでは、基礎となるすべての方程式が線形である必要があります(指数や根はありません)。受動部品(抵抗器、後でインダクターやコンデンサーなど)を扱う場合)、これは真実です。ただし、非線形であるいくつかのコンポーネント(特に特定のガス放電および半導体コンポーネント)があります。つまり、電流に対する反対が電圧および/または電流によって変化するため、これらを含む回路を呼び出します。コンポーネントの種類、非線形回路。
電力システムにおけるテベニンの定理
テベニンの定理は、回路内の1つの特定の抵抗(「負荷」と呼ばれる)が存在する電力システムやその他の回路の分析に特に役立ちます。 ”抵抗)は変更される可能性があり、回路の両端の電圧とそれを流れる電流を決定するために、負荷抵抗の各試行値で回路の再計算が必要です。回路例をもう一度見てみましょう。

R2をの「負荷」抵抗として指定するとします。この回路。R2の両端の電圧とR2を流れる電流を決定するために使用できる、4つの分析方法(分岐電流、メッシュ電流、ミルマンの定理、および重ね合わせの定理)がすでにありますが、これらの方法にはそれぞれ時間がかかります。これらの方法のいずれかを何度も繰り返して、負荷抵抗が変化した場合に何が起こるかを想像してみてください(負荷抵抗の変更は、必要に応じて複数の負荷がオン/オフされるため、電力システムでは非常に一般的です。並列接続の合計抵抗が変化します一度に接続する数によって異なります)。これには多くの作業が必要になる可能性があります。
テベニン等価回路
テベニンの定理は、負荷抵抗を一時的に除去することでこれを容易にします。元の回路と残りを同等の回路に減らす単一の電圧源と直列抵抗で構成されるcuit。次に、負荷抵抗をこの「テブナン等価回路」に再接続し、ネットワーク全体が単純な直列回路にすぎないかのように計算を実行できます。

。..テブナン変換後…
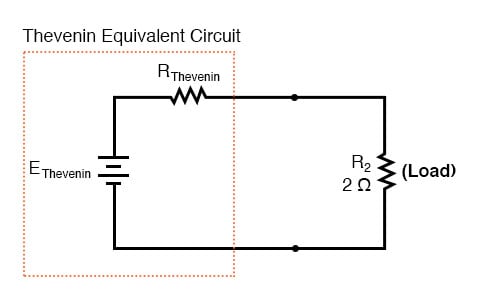
「テブナン等価回路」は、負荷抵抗(R2)が接続されている2点から見た、B1、R1、R3、およびB2の電気的等価回路です。
テブナン等価回路は、正しく導出された場合、とまったく同じように動作します。 B1、R1、R3、およびB2によって形成された元の回路。言い換えると、負荷抵抗(R2)の電圧と電流は、2つの回路の負荷抵抗の値が同じでもまったく同じである必要があります。 ETheveninとRTheveninの値が正しく計算されていれば、負荷抵抗R2は、B1、R1、R3、およびB2の元のネットワークと、ETheveninおよびRTheveninのThevenin等価回路との「違いを伝える」ことはできません。
もちろん、「テブナン変換」をより単純な回路に実行することの利点は、元のネットワークよりも負荷電圧と負荷電流を非常に簡単に解決できることです。等価テブナン電源電圧と直列抵抗の計算は実際には非常に簡単です。最初に、選択した負荷抵抗が元の回路から削除され、ブレーク(開回路)に置き換えられます。

テブナンの決定電圧
次に、負荷抵抗が取り付けられていた2点間の電圧を決定します。これを行うには、自由に使用できる分析方法を使用してください。この場合、負荷抵抗を取り除いた元の回路は、対向するバッテリーを備えた単純な直列回路にすぎないため、直列回路の規則、オームの法則、およびキルヒホフの電圧を適用することにより、開放負荷端子間の電圧を決定できます。法則:

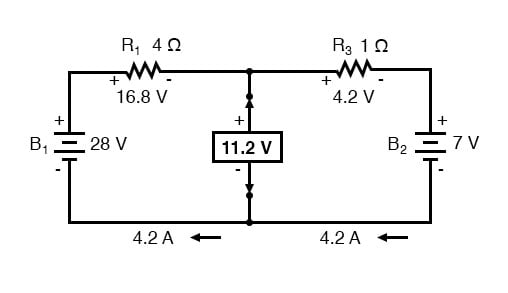
間の電圧2つの負荷接続ポイントは、バッテリーの電圧の1つと、抵抗の電圧の1つが低下し、11.2ボルトになることから計算できます。これは、等価回路の「テブナン電圧」(EThevenin)です。

テブナンの直列抵抗を決定する
同等の回路のテブナン直列抵抗を見つけるには、元の回路(負荷抵抗を取り外したまま)を取り、電源を取り外す必要があります(重ね合わせの定理で行ったのと同じスタイル:電圧源を次のように置き換えます)ワイヤと電流源をブレークに置き換え)、一方の負荷端子からもう一方の負荷端子までの抵抗を計算します。

取り外した場合2つのバッテリーのうち、この場所で測定された合計抵抗は、並列のR1とR3に等しくなります:0.8Ω。これは、等価回路の「テブナン抵抗」(RThevenin)です。

負荷抵抗の両端の電圧を決定する
接続ポイント間に負荷抵抗(2Ω)を接続すると、両端の電圧を決定できます。そして現在のネットワーク全体が単純な直列回路にすぎないかのように見えます。

R2の電圧と電流の数値に注意してください。 (8ボルト、4アンペア)は、他の分析方法を使用して検出されたものと同じです。また、テブナン直列抵抗とテブナンソース(合計)の電圧と電流の数値は、元の複雑な回路のどのコンポーネントにも適用されないことに注意してください。テブナンの定理は、ネットワーク内の単一の抵抗器、つまり負荷に何が起こるかを判断する場合にのみ役立ちます。
もちろん、その単一の抵抗器が再度多くの分析を行うことなく、2Ω以外の値。負荷抵抗の他の値をテブナンの等価回路に差し込むだけで、少しの直列回路計算で結果が得られます。
レビュー:
- テブナンの定理は、ネットワークを単一の電圧源、直列抵抗、および直列負荷で構成される同等の回路に縮小する方法です。
- テブナンの定理に従う手順:
- テブナンの定理を見つける元の回路から負荷抵抗を削除し、負荷抵抗があったオープン接続ポイント間の電圧を計算します。
- 元の回路のすべての電源を削除してテブナン抵抗を求めます(電圧源が短絡しています)。テブナン電圧源をテブナン抵抗と直列にして、テブナン等価回路を描きます。
- 負荷抵抗は、等価回路の2つのオープンポイント間に再接続します。
- 直列回路の規則に従って、負荷抵抗の電圧と電流を分析します。
関連ワークシート:
- テブナン、ノートン、および最大電力伝達定理ワークシート