A somme est le résultat dune addition. Par exemple, lajout de 1, 2, 3 et 4 donne la somme 10, écrite
 |
(1)
|
Les nombres additionnés sont appelés addends, ou parfois sommants. Lopération de sommation peut également être indiquée en utilisant un sigma majuscule avec des limites supérieure et inférieure écrites au-dessus et en dessous, et lindice indiqué ci-dessous. Par exemple, la somme ci-dessus pourrait être écrite
 |
(2)
|
Le la somme dune liste de nombres est implémentée comme Total.
Une somme
 |
(3)
|
dans lequel chaque terme 
est donné par une règle fixe (cest-à-dire, 
est un puits -séquence définie) est appelée série (finie), et si le nombre de termes 
est infini, la somme est appelée une série infinie (ou souvent juste une « série »). Une somme de la forme
 |
(4)
|
est appelée une série géométrique .
Les conditions de convergence dune série peuvent être déterminées dans le Wolfram Language en utilisant SumConvergence.
La somme des puissances finies générale
 |
(5)
|
peut être donné par lexpression
 |
(6)
|
qui équivaut à la formule de Faulhaber, où la notation 
signifie la quantité en la question est posée à la puissance appropriée 
et tous les termes de la forme 
sont remplacés par les Numéros de Bernoulli 
.
Une identité amusante due à J.Ziegenbein (pers. comm., 19 juin 2002) découle de lidentité
 |
(7)
|
qui peut être écrit
 |
(8)
|
Par conséquent, 
, par exemple, peut être écrit sous les formes équivalentes
 |
 |
 |
(9)
|
 |
 |
 |
(10)
|
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
et ainsi de suite.
Le théorème de Nicomachus donne une curieuse expression de la somme des puissances 
.
Les sommes spéciales incluent
 |
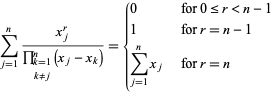(13)
|
et
 |
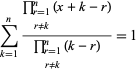(14)
|
Pour minimiser la somme dun ensemble de carrés de nombres 
sur un nombre donné 
 |
 |
 |
(15 )
|
 |
 |
 |
(16)
|
prendre la dérivée.
 |
(17)
|
La résolution de 
donne
 |
(18)
|
donc 
est minimisé lorsque 
est défini sur signifie.