Pente
En plus de sa signification familière, le mot «pente» a une signification mathématique précise. La pente dune ligne est la montée sur la course ou le changement de y divisé par le changement de x. Pour trouver la pente dune ligne, choisissez deux points quelconques sur la ligne. Puis soustrayez leurs coordonnées x et soustrayez leurs coordonnées y dans le même ordre. Divisez la différence des coordonnées y par la différence des coordonnées x:
Étant donné deux points (x1, y1) et (x2, y2) sur une ligne, la pente de la ligne est égale à:
m = =
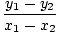
Pente négative
Si une ligne a une pente positive (cest-à-dire m > 0), alors y augmente toujours lorsque x augmente et y diminue toujours lorsque x diminue. Ainsi, le graphique de la ligne commence en bas à gauche et se dirige vers le haut à droite.
Souvent, cependant, la pente dune droite est négative. Une pente négative implique que y diminue toujours lorsque x augmente et y augmente toujours lorsque x diminue. Voici un exemple de graphique avec pente négative:
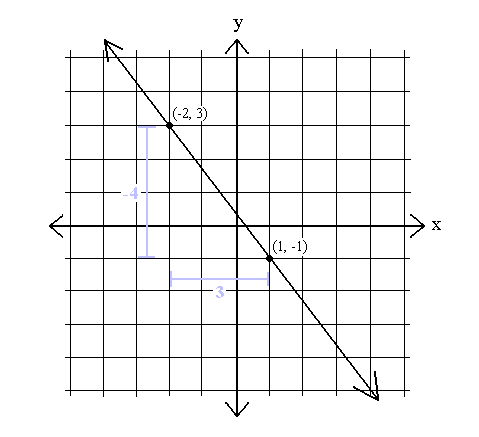
m =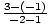 
= 
= – 
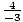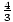
Ainsi, lorsque x augmente de 3, y diminue de 4, et lorsque x diminue de 3, y augmente de 4.
Lignes horizontales et verticales
Parfois , nous verrons des équations dont les graphiques sont des lignes horizontales. Ce sont des graphes dans lesquels y reste constant – cest-à-dire dans lesquels y1 – y2 = 0 pour deux points quelconques de la ligne:
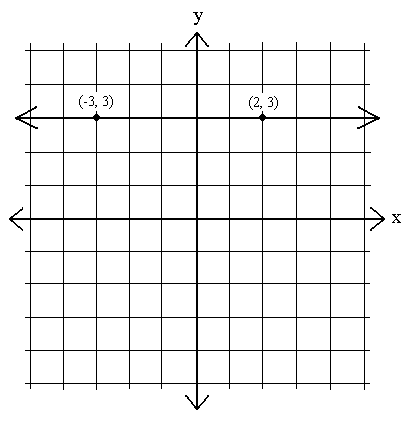
m =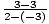 
= 
= 0.
La pente de toute ligne horizontale est 0. En dautres termes, lorsque x augmente ou diminue, y ne change pas. x prend toutes les valeurs possibles à une valeur y spécifique.
Nous verrons également des équations dont les graphiques sont des lignes verticales. Ce sont des graphiques dans lesquels x reste constant – cest-à-dire dans lesquels x1 – x2 = 0 pour deux points quelconques de la ligne:
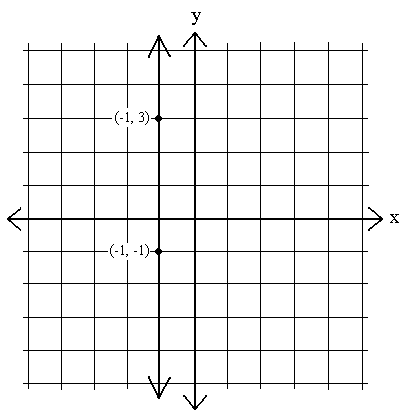
m =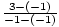 
= 
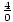= indéfini. Nous ne pouvons pas diviser un nombre par zéro.
La pente dune ligne verticale nest pas définie.x naugmente ni ne diminue; plutôt, y prend chaque valeur possible à une valeur x spécifique.