Comment la pression varie-t-elle avec le changement de volume pendant lexpansion et la compression adiabatiques dans un gaz idéal? Cette page est une annexe à notre discussion sur le son. Lair à la pression atmosphérique est un gaz presque idéal et la transmission du son dans lair est proche de ladiabatique pour les fréquences normales et les distances de transmission. (Nous revenons sur cette hypothèse ci-dessous.)
La première loi de la thermodynamique relie le changement dénergie interne dU au travail dW effectué par un système et à la chaleur dQ qui y est ajoutée.
dU = dQ – dW
Par définition, dans un processus adiabatique, la chaleur échangée dQ = 0. Remplacer ceci dans la première loi et réorganiser donne
0 = dQ = dU + dW
Le deuxième terme est simple: le travail effectué dW lorsquun système change son volume V par dV est PdV.
Le premier terme peut être lié à la chaleur spécifique, qui est définie comme la chaleur ajoutée par unité de changement de température par mole de substance. Si nous ajoutons de la chaleur à volume constant, alors le gaz ne se dilate pas et ne fonctionne donc pas. Ainsi, la chaleur ajoutée augmente lénergie interne U. Il sensuit donc cette définition que la chaleur spécifique à volume constant est ![]() , où n est le nombre de moles. Doù
, où n est le nombre de moles. Doù
Maintenant léquation détat dun gaz parfait est
nRT = PV ( ii)
où R est la constante du gaz. Prendre des dérivées donne
Nous pouvons maintenant combiner les équations (i) et (iii) pour éliminer T. (i) et (ii) donner respectivement ces expressions pour ncv dT:
La collecte des termes PdV et VdP donne
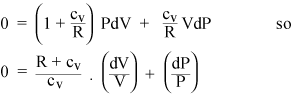
Maintenant si le gaz est idéal, son énergie interne est entièrement cinétique, donc lénergie interne U ne dépend que de T. A partir de léquation détat dun gaz idéal (ii), on peut calculer le travail dW fait à pression constante: il sagit simplement de PdV = nRdT. Donc, si nous ajoutons de la chaleur à un gaz à pression constante, nous devons ajouter de la chaleur RdT pour chaque mole de gaz, au-delà de la chaleur quil faudrait ajouter à volume constant. Ainsi, la chaleur spécifique dun gaz parfait à pression constante est juste cP = cv + R. Le rapport des chaleurs spécifiques est donné par un symbole standard:
. Nous avons donc
(iv)
Cest le résultat principal dont nous avons besoin pour discuter des ondes sonores: nous venons de montrer que le changement proportionnel de pression est – γ fois le changement proportionnel de volume ou γ fois le changement proportionnel de densité.
Ne nous arrêtons pas ici, cependant, car nous ne sommes quà quelques lignes dun résultat important. Nous savons que d (ln x) = dx / x (voir calcul pour une preuve). Nous pouvons donc écrire léquation précédente comme
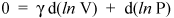
et réorganisez-le pour donner
(v)
Donc pour un processus adiabatique dans un gaz parfait,
. (vi)
Après réflexion, vous « conviendrez que cP > cV: At volume constant, tout e La chaleur que vous mettez sert à augmenter lénergie interne et donc à augmenter la température. À pression constante, vous devez introduire non seulement la chaleur qui augmente lénergie interne, mais également une quantité de chaleur égale au travail effectué lorsque le système subit une dilatation thermique. Pour lair, γ est denviron 1,4.
Bien sûr, nous pouvons maintenant substituer dans (vi) léquation de létat (ii) pour voir comment P et T ou T et V sont liés pour un processus adiabatique.
Quand le son est-il adiabatique?
Nous avons mentionné plus haut que « la transmission du son dans lair est proche de ladiabatique pour les fréquences normales et les distances de transmission ». Quand cela échoue-t-il? Aux maxima de pression dans une onde sonore, la température est élevée. Nous nous attendons donc à ce quune partie de la chaleur se diffuse vers les minima de pression voisins. Bien sûr, en une demi-période donde sonore, il ny a pas beaucoup de temps pour que la chaleur diffuse une demi-longueur donde. Cependant, le temps nécessaire à la diffusion de la chaleur correspond au carré de la distance. Ce processus est donc moins négligeable pour les hautes fréquences, car la demi-longueur donde plus courte compense largement la demi-période plus courte. Cette diffusion prend lénergie mécanique de londe, en particulier aux fréquences élevées, et leffet augmente avec la distance de transmission.Pour cette raison (et parfois pour dautres), les sons distants sont non seulement moins forts, mais aussi moins brillants que les sons proches.