Quoi est lalgorithme BFS (recherche en largeur dabord)?
La recherche en largeur dabord (BFS) est un algorithme utilisé pour représenter graphiquement des données ou rechercher des arbres ou traverser des structures. La forme complète de BFS est la recherche en largeur dabord.
Lalgorithme visite et marque efficacement tous les nœuds clés dun graphe de manière précise dans le sens de la largeur. Cet algorithme sélectionne un seul nœud (point initial ou source) dans un graphique, puis visite tous les nœuds adjacents au nœud sélectionné. Noubliez pas que BFS accède à ces nœuds un par un.
Une fois que lalgorithme visite et marque le nœud de départ, il se déplace vers les nœuds non visités les plus proches et les analyse. Une fois visités, tous les nœuds sont marqués. Ces itérations se poursuivent jusquà ce que tous les nœuds du graphe aient été visités et marqués avec succès.
Dans ce didacticiel sur lalgorithme, vous apprendrez:
- Quest-ce que lalgorithme BFS (Breadth-First Search)?
- Quest-ce que les traversées de graphes?
- Larchitecture de lalgorithme BFS
- Pourquoi avons-nous besoin de lalgorithme BFS?
- Comment fonctionne lalgorithme BFS?
- Exemple dalgorithme BFS
- Règles de lalgorithme BFS
- Applications de lalgorithme BFS
Quest-ce que les traversées de graphes?
Un parcours de graphe est une méthodologie couramment utilisée pour localiser la position du sommet dans le graphe. Cest un algorithme de recherche avancé qui peut analyser le graphique avec rapidité et précision tout en marquant la séquence des sommets visités. Ce processus vous permet de visiter rapidement chaque nœud dun graphe sans être enfermé dans une boucle infinie.
Larchitecture de lalgorithme BFS
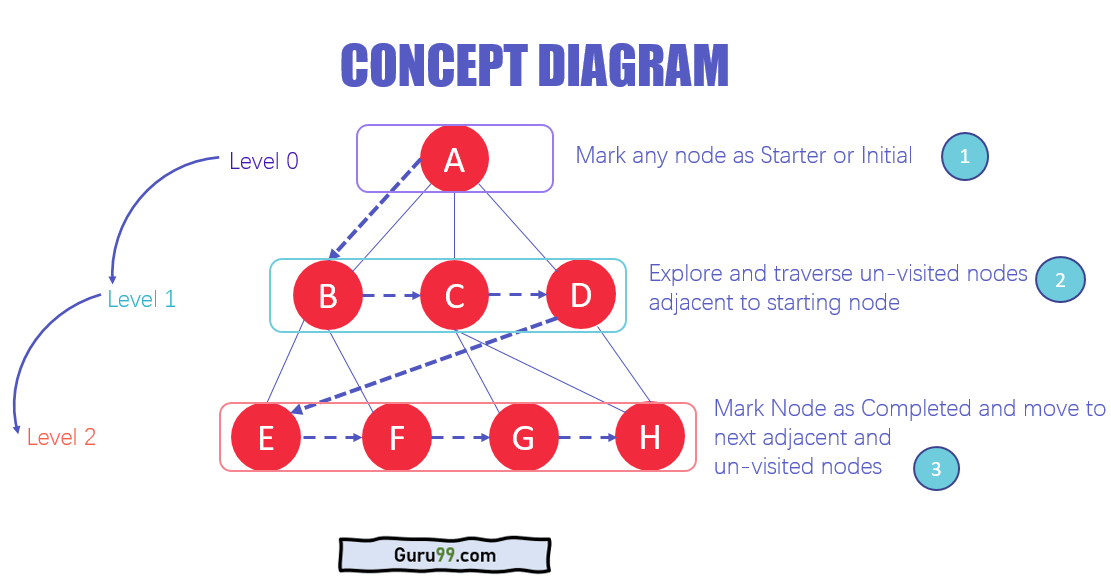
- Dans les différents niveaux de données, vous pouvez marquer nimporte quel nœud comme point de départ ou le nœud initial à parcourir. Le BFS visitera le nœud et le marquera comme visité et le placera dans la file dattente.
- Maintenant, le BFS visitera les nœuds les plus proches et non visités et les marquera. Ces valeurs sont également ajoutées à la file dattente. La file dattente fonctionne sur le modèle FIFO.
- De la même manière, les nœuds les plus proches et non visités restants sur le graphique sont analysés marqués et ajoutés à la file dattente. Ces éléments sont supprimés de la file dattente en tant que réception et imprimés en conséquence.
Pourquoi avons-nous besoin de lalgorithme BFS?
Il existe de nombreuses raisons dutiliser lalgorithme BFS pour rechercher votre ensemble de données. Certains des aspects les plus vitaux qui font de cet algorithme votre premier choix sont:
- BFS est utile pour analyser les nœuds dun graphe et construire le chemin le plus court pour les traverser.
- BFS peut parcourir un graphe dans le plus petit nombre ditérations.
- Larchitecture de lalgorithme BFS est simple et robuste.
- Le résultat de lalgorithme BFS possède un haut niveau de précision par rapport à dautres algorithmes.
- Les itérations BFS sont transparentes, et il ny a aucune possibilité que cet algorithme soit pris dans un problème de boucle infinie.
Comment fonctionne lalgorithme BFS?
La traversée de graphe nécessite que lalgorithme visite, vérifie et / ou met à jour chaque nœud non visité dans une structure arborescente. Les parcours de graphe sont classés en fonction de lordre dans lequel ils visitent les nœuds sur le graphe.
Lalgorithme BFS démarre lopération à partir du premier nœud ou du nœud de départ dun graphe et le parcourt en profondeur. Une fois quil a traversé avec succès le nœud initial, le prochain sommet non traversé du graphe est visité et marqué.
Par conséquent, vous pouvez dire que tous les nœuds adjacents au sommet courant sont visités et traversés dans la première itération. Une méthodologie de file dattente simple est utilisée pour implémenter le fonctionnement dun algorithme BFS, et elle comprend les étapes suivantes:
Étape 1)

Chaque sommet ou nœud du graphe est connu. Par exemple, vous pouvez marquer le nœud comme V.
Étape 2)

Dans le cas où le sommet V nest pas accessible, ajoutez le sommet V dans la file dattente BFS
Étape 3)

Démarrez la recherche BFS, et après la fin, marquez le sommet V comme visité.
Étape 4)

La file dattente BFS est toujours pas vide, supprimez donc le sommet V du graphe de la file dattente.
Étape 5)

Récupérer tous les sommets restants sur le graphe adjacent au sommet V
Étape 6)

Pour chaque sommet adjacent, disons V1, au cas où il ne serait pas encore visité, ajoutez V1 à la file dattente BFS
Étape 7)

BFS visitera la V1, la marquera comme visitée et la supprimera de la file dattente.
Exemple dalgorithme BFS
Étape 1)

Vous avez un graphique de sept nombres allant de 0 à 6.
Étape 2)

0 ou zéro a été marqué comme nœud racine.
Étape 3)

0 est visité, marqué et inséré dans la structure de données de la file dattente.
Étape 4)
Les 0 nœuds adjacents et non visités restants sont visités, marqués et insérés dans la file dattente.
Étape 5)

Les itérations de déplacement sont répétées jusquà ce que tous les nœuds soient visités.
Règles de lalgorithme BFS
Voici des règles importantes pour lutilisation de lalgorithme BFS:
- Une structure de données de file dattente (FIFO-First in First Out) est utilisé par BFS.
- Vous marquez nimporte quel nœud du graphique comme racine et commencez à parcourir les données à partir de celui-ci.
- BFS parcourt tous les nœuds du graphique et continue de les déposer comme terminés.
- BFS visite un nœud non visité adjacent, le marque comme terminé et linsère dans une file dattente.
- Supprime le sommet précédent de la file dattente au cas où aucun sommet adjacent ne serait trouvé.
- Lalgorithme BFS effectue une itération jusquà ce que tous les sommets du graphe soient traversés avec succès et marqués comme terminés.
- Il ny a pas de boucles causées par BFS lors de la traversée des données à partir de nimporte quel nœud.
Applications de lalgorithme BFS
Prenons un Regardez quelques-unes des applications réelles où une implémentation dalgorithme BFS peut être très efficace.
- Graphiques non pondérés: lalgorithme BFS peut facilement créer le chemin le plus court et un arbre couvrant minimum pour tout visiter les sommets du graphe dans les plus brefs délais avec une grande précision.
- Réseaux P2P: BFS peut être implémenté pour localiser tous les nœuds les plus proches ou voisins dans un réseau peer to peer. Cela permettra de trouver les données requises plus rapidement .
- Crawlers Web: les moteurs de recherche ou les robots dexploration Web peuvent facilement créer plusieurs niveaux dindex en utilisant BFS. La mise en œuvre de BFS commence à partir de la source, qui est la page Web, puis il visite tous les liens de cette source .
- Systèmes de navigation: BFS peut aider à trouver tous les emplacements voisins à partir de lemplacement principal ou source.
- Diffusion réseau ing: Un paquet diffusé est guidé par lalgorithme BFS pour trouver et atteindre tous les nœuds pour lesquels il a ladresse.
Résumé
- Un parcours de graphe est un processus unique qui nécessite que lalgorithme visite, vérifie et / ou met à jour chaque nœud non visité dun structure arborescente. Lalgorithme BFS fonctionne sur un principe similaire.
- Lalgorithme est utile pour analyser les nœuds dun graphe et construire le chemin le plus court pour les traverser.
- Lalgorithme parcourt le graphe dans le plus petit nombre ditérations et le temps le plus court possible.
- BFS sélectionne un seul nœud (point initial ou source) dans un graphique, puis visite tous les nœuds adjacents au nœud sélectionné. BFS accède à ces nœuds un par un.
- Les données visitées et marquées sont placées dans une file dattente par BFS. Une file dattente fonctionne sur la base du premier entré, premier sorti. Par conséquent, lélément placé en premier dans le graphique est dabord supprimé et imprimé en conséquence.
- Lalgorithme BFS ne peut jamais être pris dans une boucle infinie.
- En raison de sa haute précision et de sa mise en œuvre robuste, BFS est utilisé dans plusieurs solutions réelles telles que les réseaux P2P, les robots dexploration Web, et diffusion en réseau.