Supposons que lair est pompé dans un tube rond lisse, qui a un diamètre constant à lexception dune section au milieu où le tube se rétrécit jusquà la moitié du diamètre, puis sélargit à nouveau. Supposons que tous les changements de diamètre se déroulent en douceur et que lair circule régulièrement dans le tube, sans tourbillons ni turbulences.
Exercice
où dans le tube vous attendez-vous la pression pour être la plus grande?
Réponse
La plupart des gens ont posé cette question pour la première fois et prédisent que la pression sera la plus élevée dans la partie étroite du tube. Mais en fait, si nous faisons réellement lexpérience, en plaçant des manomètres en différents points le long du tube, nous constatons, contre-intuitivement, que la pression de lair est la plus basse là où lair se déplace le plus rapidement!

Pour voir comment cela pourrait être, nous allons appliquer les techniques que nous avons développées pour déterminer comment la pression variait dans un fluide stationnaire. La façon dont nous avons fait cela, rappelez-vous, était de dessiner un diagramme de corps libre pour un petit cylindre de fluide. Comme ce petit cylindre était au repos, la force totale sur lui était nulle, donc la pression nette équilibrait le poids. Considérons maintenant un fluide en mouvement constant. Il est utile de visualiser le flux en dessinant des lignes fluides, des lignes telles que leur direction soit la direction dans laquelle le fluide se déplace à chaque point.

En fait, ces lignes de courant vous indiquent non seulement la direction dans laquelle le fluide se déplace, mais donnent également une idée de la vitesse – là où elles se rapprochent, le fluide doit se déplacer plus rapidement, car la même quantité de fluide sécoule à travers une région plus étroite. Imaginez maintenant un cylindre dair se déplaçant le long du tuyau, son axe parallèle à la ligne de courant. Évidemment, il doit accélérer lorsquil entre dans la partie étroite du tube – puisque la même quantité dair circule dans la partie étroite que dans la partie large, il doit aller plus vite.
Mais si le petit le cylindre de fluide accélère, il doit être actionné par une force qui le pousse par derrière.
Son poids na pas dimportance ici, car il se déplace horizontalement. Par conséquent, la seule force agissant sur lui est la pression, et nous devons en conclure que la pression à son dos est supérieure à la pression sur son front. Par conséquent, la pression doit chuter en entrant dans la partie étroite. Pour clarifier ce qui se passe, nous allons dessiner un cylindre assez grand:
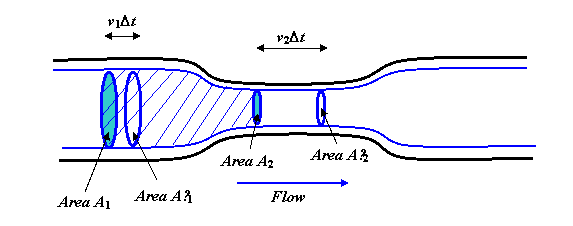
Le fluide circule régulièrement et en douceur le tuyau. Les lignes bleues épaisses sont des lignes fluides, en fait, vous devriez imaginer faire pivoter tout le diagramme autour de laxe central pour obtenir une image en trois dimensions, et les lignes bleues deviendraient un cylindre, avec une section plus étroite en «cou», faisant écho à la forme du
Considérons maintenant le corps de fluide dans les lignes de courant indiquées, et coiffé aux deux extrémités par les zones circulaires A1 et A2. Le débit de fluide à travers A1 doit être le même que le débit de à travers A2, car en débit constant, le fluide ne peut pas saccumuler au milieu (ou sépuiser à partir de là non plus). Le volume qui traverse A1 en une seconde est v1A1. (Pour voir cela, imaginez un long tuyau droit sans Si le fluide sécoule à, disons 3 mètres par seconde, alors en une seconde, tout le fluide qui se trouvait à moins de 3 mètres de la zone A1 en amont aura traversé.)
Donc, flux à travers A1 équivaut à flux à travers A2, \
(Note de bas de page: il est peut-être intéressant de mentionner que nous supposons implicitement les véloci ty est le même en tous points sur la zone A1. Tout fluide réel a une certaine viscosité (friction) et se déplacera plus lentement près des côtés du tuyau quau milieu. Nous en discuterons plus tard. Pour linstant, nous considérons un fluide « idéal », le terme utilisé quand on ignore la viscosité. En fait, le résultat que nous en tirons est ok – nous aurions pu prendre une petite zone A1 loin des côtés, de sorte que la vitesse aurait été pareil pour toute la zone, mais cela aurait donné un diagramme beaucoup moins clair.)
Nous sommes maintenant prêts à examiner laugmentation de lénergie cinétique du fluide à mesure quil accélère dans la partie étroite, et comprendre comment la différence de pression a fait le travail nécessaire pour laccélérer.
\
La seule source possible de cette augmentation dénergie est le travail effectué par la pression pour pousser le fluide dans la partie étroite.
\
Cest donc un travail effectué sur notre morceau de fluide par le fluide qui le pousse par derrière – mais ce nest pas la fin de lhistoire, car notre morceau de le fluide lui-même travaille en poussant le fluide devant lui, donc pour trouver laugmentation totale de lénergie de notre morceau, nous devons soustraire le travail externe quil fait.Autrement dit, le travail total effectué par pression sur notre fluide est
\
en se souvenant que \ (A_1v_1 = A_2v_2 \).
Ce travail doit être égal le changement dénergie cinétique, donc
\
doù
\
Cest léquation de Bernoulli.
\.
Contributeurs et attributions
- Michael Fowler (Beams Professor, Department of Physics, University of Virginia)